bipartite matching

Bipartite Matching(이분 매칭)

1. Graph Mathcing

Graph의 Mathcing이란 단순 그래프가 주어졌을 때 끝점을 공유하지 않는 간선의 집합을 표현하는 방법이다. 아래 사진은 올바른 매칭이 진행되었을 때 결과이다.

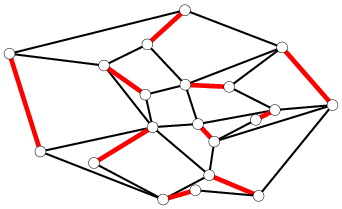
이 때 가장 큰 매칭을 찾아내는 문제를 최대 매칭 문제라고한다. 하지만 가장 General한 Mathcing 알고리즘은 꽤나 복잡하여 알고리즘 대회에서는 좀 더 단순한 형태로 등장하게 된다.

2. 이분매칭

이분 그래프란 정점을 두 그룹으로 나누어 모든 간선이 서로 다른 그룹의 정점들을 연결하도록 할 수 있는 그래프다. 이분 그래프는 두 집합의 대응 관계를 표현하기 위해 흔히 사용된다.

작업 분담, 사람을 짝짓는 방법 등 현실세계에서 직관적인 의미를 가지기 때문에 이분 매칭은 매칭 알고리즘 중에서 따로 언급할 가치가 있다.

3. 구현

#include<iostream>
#include<vector>

using namespace std;

const int MAX_N = 1000, MAX_M = 1000;

//A와 B의 정점의 개수
int n, m;
//인접리스트
bool adj[MAX_N][MAX_M];
//각 정점에 매칭된 상대 정점의 번호를 저장한다.
vector<int> aMatch, bMatch;
//dfs 방문 여부
vector<bool> visited;
//A의 정점인 a에서 B의 매칭되지 않은 정점으로 가는 경로를 찾는다.
bool dfs(int a) {
	if (visited[a]) return false;
	visited[a] = true;
	for (int b = 0; b < m; b++) {
		if (adj[a][b]) {//b가 이미 매칭되어 있다면 bMatch[b]에서부터 시작해 증가경로를 찾는다
			if (bMatch[b] == -1 || dfs(bMatch[b])) {
				//증가 경로를 발견할 경우 a와 b를 매치 시킨다
				aMatch[a] = b;
				bMatch[b] = a;
				return true;
			}
		}
	}

	return false;
}

int bipartiteMatch() {
	//처음에는 정점이 모두 연결되어 있지 않음.
	aMatch = vector<int>(n, -1);
	bMatch = vector<int>(m, -1);
	int size = 0;
	for (int start = 0; start < n; start++) {
		visited = vector<bool>(n, false);
		if (dfs(start))
			++size;
	}
	return size;
}

포드-풀커슨 알고리즘을 통해 이분 매칭을 구현할 수도 있지만, 이분 매칭 문제는 일반적인 네트워크 유량 문제보다 비교적 자주 출현하기 때문에 좀 더 간단한 형식의 코드를 작성해둘 필요가 있다.

작성된 코드는 이분매칭의 관련된 속성으로 인해 동작한다.

1. 최대 유량이 \(O(\left\lvert V \right\rvert)\)로 고정된다. 포드 풀커슨 알고리즘을 이용한 구현은 수행시간이 최대 유량에 비례하므로, 깊이 우선 탐색을 사용하여도 될 것이다.
2. 증가 경로를 찾기 위해 탐색하는 도중 B에 포함된 정점에 도착했는데 이 정점이 이미 매칭된 상황이라면, 증가 경로의 다음 간선은 유일하게 결정된다.
   • 싱크로 나가는 간선 하나 밖에 없는 경우이고, 매칭된 상황에서는 이 간선의 잔여용량이 남아있지 않을 것이다.
   • 이는 곧 매칭된 정점 A로 유량을 상쇄하는 방법 밖에 남지 않았다는 것이다.
   • 따라서, b와 인접한 정점을 확인하는 것이 아니라 매칭된 a를 곧장 재귀호출 하는 부분은 위와 같은 속성을 이용한 것이다.

4. 문제 BISHOPS

링크: https://algospot.com/judge/problem/read/BISHOPS \

input

입력은 여러 개의 테스트 케이스로 주어진다. 입력의 첫 줄에는 테스트 케이스의 개수 \(T\)가 들어온다. 각각의 테스트 케이스의 첫 줄에는 체스판의 크기 \(N (1 \le N \le 8)\)이 주어진다. 이후 N줄에는 체스판의 상태가 주어진다. . 은 Bishop을 놓을 수 있는 곳이며, * 은 장애물이다.

output

각각의 테스트 케이스들에 대해 최대로 놓을 수 있는 Bishop의 개수를 출력한다.

Test Case

3
5
.....
.....
.....
.....
.....
8
..**.*.*
**.***.*
*.**...*
.*.**.**
*.**.*.*
..**.*.*
...*.*.*
**.*.*.*
8
*.*.*.*.
.*.*.*.*
*.*.*.*.
.*.*.*.*
*.*.*.*.
.*.*.*.*
*.*.*.*.
.*.*.*.*

8
18
7

코드

#include<iostream>
#include<vector>
#include<string>
#include<string.h>

using namespace std;

const int MAX_CHESS_BOARD_SIZE = 8, MAX = 100;

int T, N, n, m;
string chessboard[MAX_CHESS_BOARD_SIZE + 2];
int id[2][MAX_CHESS_BOARD_SIZE + 2][MAX_CHESS_BOARD_SIZE + 2], adj[MAX][MAX];
int dy[2] = { 1, 1 }, dx[2] = { 1, -1 };
vector<int> match;
vector<bool> visited;

bool dfs(int a) {
	if (visited[a]) return false;
	visited[a] = true;
	for (int b = 1; b < m; b++) {
		if (adj[a][b]) {//b가 매칭되어 있지 않거나 이미 매칭된 정점이 다른 정점과 매칭이 가능할 경우 bMatch[b]에서부터 시작해 증가경로를 찾는다
			if (match[b] == -1 || dfs(match[b])) {
				//증가 경로를 발견할 경우 a와 b를 매치 시킨다
				match[b] = a;
			//	cout << a << "와 " << b << "를 매칭시킵니다." << endl;
				return true;
			}
		}
	}

	return false;
}

int bipartiteMatch() {
	//처음에는 정점이 모두 연결되어 있지 않음.

	match = vector<int>(m, -1);
	int size = 0;
	for (int start = 1; start < n; start++) {
		visited = vector<bool>(n, false);
		if (dfs(start))
			++size;
	}
	return size;
}


void binding() {
	//starting number for each node is 1.
	int idx[2] = { 1, 1 };

	for (int direction = 0; direction < 2; direction++) {
		int visited[MAX_CHESS_BOARD_SIZE + 2][MAX_CHESS_BOARD_SIZE + 2];
		memset(visited, false, sizeof(visited));
		for (int y = 1; y <= N; y++) {
			for (int x = 1; x <= N; x++) {
				int cy = y, cx = x;
				//verify that we have not visited, and can create nodes
				while (chessboard[cy][cx] != '*' && !visited[cy][cx]) {
					visited[cy][cx] = true;
					//numbering
					id[direction][cy][cx] = idx[direction];
					cy += dy[direction];
					cx += dx[direction];
				}
				idx[direction]++;
			}
		}
	}
	n = idx[0];
	m = idx[1];
}


int main() {
	ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);

	cin >> T;
	while (T-- > 0) {

		//input
		cin >> N;		
		for (int i = 1; i <= N; i++) {
			cin >> chessboard[i];
			chessboard[i] = "*" + chessboard[i] + "*";
		}

		//init
		chessboard[N + 1] = "**********";
		chessboard[0] = "**********";
		memset(adj, 0, sizeof(adj));
		memset(id, 0, sizeof(id));

		//creating nodes.
		binding();
		//connecting edges.
		for (int y = 1; y <= N; y++) {
			for (int x = 1; x <= N; x++) {
				if (chessboard[y][x]) {
					adj[id[0][y][x]][id[1][y][x]] = 1;
				}
			}
		}

		//bipartite matching
		int Answer = bipartiteMatch();

		//output
		cout << Answer << "\n";

	}

}

핵심 아이디어

문제의 핵심이 되는 접근법은 대각선 방향으로 체스판을 묶는 것이다. 아래 그림과 같이 체스판을 묶을 경우 빈칸은 두 종류의 대각선 방향으로 나타낼 수 있다.

따라서, 이와 같이 그래프를 구성할 경우 비숍을 놓는다 == 두 묶음을 서로 대응시킨다로 나타낼 수 있다.

Refernce

• 구종만 지음, 알고리즘 문제 해결 전략, 인사이트, 32장