closest pair

definition

• input: \(p_1, p_2, p_3, ... p_n\) \((p_i = (x_i, y_i))\)
• output: \(p_i, p_j\) with smallest \(p_i - p_j\)

Brute-force algorithm

minDist = infinity
for i = 1 to length(P) - 1 do
    for j = i + 1 to length(P) do
        let p = P[i], q = P[j]
        if dist(p, q) < minDist  then
            minDist = dist(p, q)
            closestPair = (p, q)
return closestPair

time complexity: \(O(n^2)\)

Divide and Conquer algorithm

1. 점들을 x좌표에 따라 정렬한다.
2. 점들이 두개의 같은 크기의 집합으로 나뉘도록 수직선 \(x = x_mid\)를 기준으로 양옆으로 분할한다.
3. 왼쪽과 오른쪽의 점들의 집합에 대해 재귀적으로 문제를 해결한다. 이것을 통해 왼쪽과 오른쪽에서의 최근접 거리인 \(d_{Lmin}\)과 \(d_{Rmin}\)을 찾을 수 있다.
4. 분할선 기준으로 나뉜 쌍들이 존재할 수 있으므로 중간에 존재하는 쌍들 중 거리가 최소가 되는 \(d_{LRmin}\)을 구한다.
5. 최종적으로 찾고자 하는 최근접 거리는 \(d = min(d_{Lmin}, d_{Rmin}, d_{LRmin})\)이다.

time complexity

시간복잡도의 가장 영향을 미치는 부분인 4번 항목에 대해 알아보자.

우선 먼저 생각해야하는 것은 최악의 경우에도 \(d = min(d_{Lmin}, d_{Rmin})\) band 내에서는 \(n^2\) 미만의 점을 가진다. 또한 각점에 대해 반대편에 확인해야 할 점의 개수는 최대 6개이다. 따라서, \(6n\)의 계산시간이 필요하다. 이에 대한 자세한 설명은 아래 Lemma 항목을 참고

이 알고리즘의 연산의 수행 횟수를 재귀식으로 표현한다면 \(T(n) = 2T(n/2) + O(n)\)으로 표현할 수 있으며 마스터 정리에 따라 \(O(nlogn)\)이다.

Lemma

\(Claim\): A rectangle of width \(d\) and height \(2d\) can contain at most six points such that any two points are at distance at least \(d\)

\(Proof\): This will be an intuitive proof by construction. We shall begin to place points into the box until it is impossible to add any more. First imagine a circle of radius d around each point representing the area that we are not allowed to insert another point into. We can minimize the overlapping area of such a circle with the rectangle by placing the point on the corner of the rectangle as in the following figure:

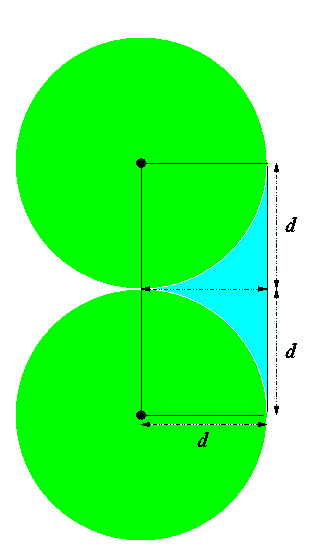
Hence we can place points somewhere inside the light blue area or on the edges of the circles. Hence we put one more in the middle of the left side leaving the entire box covered except for the remaining two corners and the middle of the right side (all three of these points being right on the boundaries of the circles). Once we do this we have the following structure:

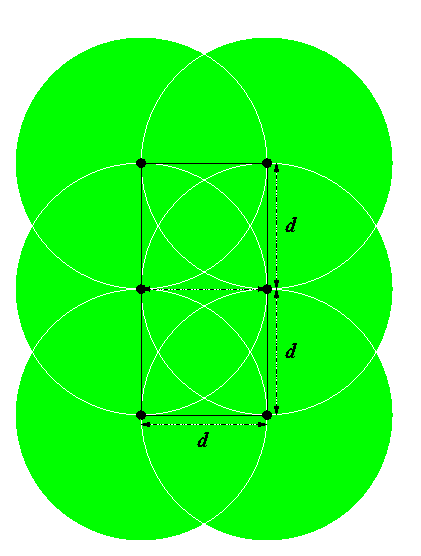
Note that there are now six points in the square. If you try to move any one of these points in any direction within the boundaries of the rectangle, then you would be moving two points too close toghether.

Hence we can’t possibly add any more points to this rectangle without putting violating the distance property between the points. Therefore six is the maximum number of points we can have.

Refernce

• https://en.wikipedia.org/wiki/Closest_pair_of_points_problem
• https://sites.cs.ucsb.edu/~suri/cs235/ClosestPair.pdf
• https://www.cs.mcgill.ca/~cs251/ClosestPair/proofbox.html