covex hull

Graham Scan

pseudo code

sort by y-order; //$$p_1, p_2, ..., p_n$$
stack.push($$p_1, p_2$$);
for i = 3 to $$n$$ do
  while next $$\angle next, top, $$p_i$$ != CCW
    stack.pop()
  stack.push($$p_i$$)
return stack

Analysis of Graham Scan

1. Invariant \(<p_1, ... ,stack.top()>\) is convex
2. 기울기 공식: \(D = det\begin{vmatrix} 1 & p_x & p_y \\ 1 & q_x & q_y \\ 1 & r_x & r_y \end{vmatrix}\)
   • if \(D > 0\) then \(\angle p, q, r\) is CCW
   • else if \(D < 0\) \(\angle p, q, r\) is CW
   • else then \(\angle p, q, r\) is straight
   • \(D = p \cdot (q \times r)\) 이다.
3. 정렬 이후 \(O(n)\)번의 스캔이 일어나며 반복 수행마다 \(logn\)의 시간 소요
   • time complexity: \(O(nlogn)\)

Divide and Conquer

pseudo code

• sort by x-order
• Let \(A\) be the set of \(n/2\) leftmost points and \(B\) the set of \(n/2\) rightmost points
• Reculsively compute \(CovexHull(A)\) and \(ConvexHull(B)\)
• Merge to obtain CovexHull(S)
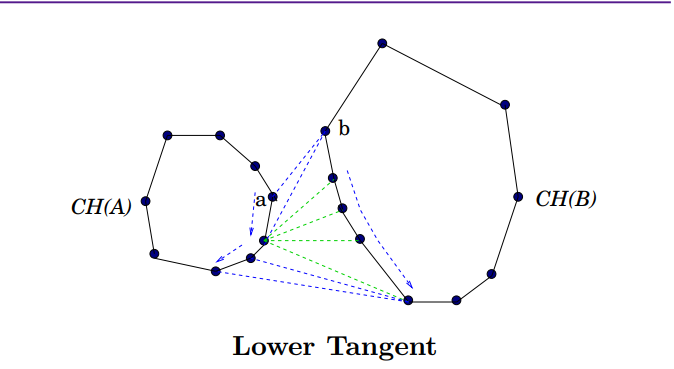
  • a = rightmost point of \(CovexHull(A)\)
  • b = leftmost point of \(ConvexHull(B)\)
  • while \(\overline{ab}\) not lower tangent of \(CovexHull(A)\) and \(ConvexHull(B)\)
    1. while \(\overline{ab}\) not lower tangent to :\(ConvexHull(A)\)
       • set \(a = a-1\)(move \(a\) \(CW\))
    2. while \(\overline{ab}\) not lower tangent to :\(ConvexHull(B)\)
       • set \(b = b+1\)(move \(b\) \(CCW\))
• return \(\overline{ab}\)

Analysis of Divide and conquer

• 처음 정렬에 걸리는 시간 \(O(nlong)\)
• . \(T(N) = 2T(N/2) + O(N)\)
• Merge 즉, 합치는 데 걸리는 시간은 선형이다.
• 마스터 정리에 의하여 \(T(N) = O(nlogn)\)

Refernce

• https://sites.cs.ucsb.edu/~suri/cs235/ConvexHull.pdf