parallel binary search

parallel binary search

어떤 문제가 요구하는 정답이 단조 증가 모양을 가질 때 이를 이용하여 답을 빠르게 구할 수 있다.

단조 증가하며, 순서대로 진행하는 쿼리 \(Q = {q_1, q_2, ... q_n}\)이 있다 하자.

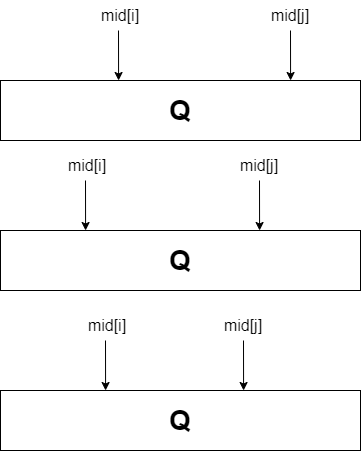
위 그림과 같이 쿼리에 대하여 binary search를 진행할 수 있는 경우, 문제공간에 대해 병렬 이분 탐색을 진행할 수 있다.

음악 추천

입력

입력의 첫째 줄에는 세 정수로, 곡의 수 N(2 ≤ N ≤ 100,000), 추천 알고리즘의 결과 데이터의 수 K(1 ≤ K ≤ 100,000), 목표 점수 J(10 ≤ J ≤ 108)가 주어진다. 각각의 곡은 1번부터 N번까지 번호가 붙어 있다. 다음 줄에 N-1개의 곡 번호가 주어지는데, 이는 2번 곡부터 해당 곡의 부모 노드가 되는 곡의 번호이다. 1번 곡은 부모 노드가 없다. 다음 줄에 N개의 수가 주어지는데, 이는 1번 곡부터 해당 곡을 부른 가수의 번호이다. 가수의 번호는 1 이상 N 이하의 자연수이다. 다음 K개의 줄에 추천 알고리즘의 결과 데이터가 하나씩 주어진다. 결과 데이터는 T, P, S의 세 값으로 주어진다. T는 데이터가 계산된 시간으로, 1 이상 109 이하의 자연수이다. P는 점수가 부여되는 서브트리의 루트가 되는 곡의 번호이다. S는 서브트리에 부여할 가중치로, 1 이상 109 이하의 자연수이다.

출력

출력은 N개의 줄로 이루어진다. 1번 곡부터 해당 곡을 부른 가수의 평균 점수가 J를 넘게 되는 시간을 출력한다. 점수가 J를 넘는 일이 없는 경우 -1을 출력한다. 같은 가수가 부른 곡은 같은 값을 가지게 될 것이다.

코드

#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>

#include<map>
typedef long long ll;

using namespace std;

const int MAX = 100000 + 2, MAX_VALUE = 1e+9, MAX_J = 1e+8, MAX_T = 1e9 + 1;

struct Query {
	int t, p, s;
};

struct Node {
	int parent, index, artist, descendants;
};

int N, K, T, P, S, parent, n, artist, order[MAX], lo[MAX], hi[MAX], answer[MAX];
ll seg[4 * MAX], lazy[4 * MAX], score[MAX], J;
Node tree[MAX];
Query queries[MAX];
vector<int> children[MAX], pbs[MAX], songs[MAX];


void update_lazy(int node, int left, int right) {
	if (lazy[node] == 0) return;
	seg[node] += (right - left + 1) * lazy[node];
	if (left != right) {
		lazy[node * 2] += lazy[node];
		lazy[node * 2 + 1] += lazy[node];
	}
	lazy[node] = 0;
}

ll update(int lo, int hi, ll value, int node, int left, int right) {
	update_lazy(node, left, right);
	if (right < lo || hi < left) {
		return seg[node];
	}
	if (lo <= left && right <= hi) {
		lazy[node] += value;
		update_lazy(node, left, right);
		return seg[node];
	}

	int mid = (left + right) / 2;
	return seg[node] = update(lo, hi, value, 2 * node, left, mid) + update(lo, hi, value, 2 * node + 1, mid + 1, right);
}

ll sum(int lo, int hi, int node, int left, int right) {
	update_lazy(node, left, right);
	if (right < lo || hi < left) {
		return 0;
	}
	if (lo <= left && right <= hi) {
		return seg[node];
	}

	int mid = (left + right) / 2;
	return sum(lo, hi, 2 * node, left, mid) + sum(lo, hi, 2 * node + 1, mid + 1, right);
}

int dfs(int cur) {
	order[cur] = ++n;
	tree[cur].index = n;
	for (auto child : children[cur]) {
		tree[cur].descendants += dfs(child);
	}
	return tree[cur].descendants + 1;
}

int main() {

	//FAST IO
	ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);

	cin >> N >> K >> J;
	for (int i = 2; i <= N; i++) {
		cin >> parent;
		tree[i].parent = parent;
		children[parent].push_back(i);
	}
	for (int i = 1; i <= N; i++) {
		cin >> artist;
		songs[artist].push_back(i);
		tree[i].artist = artist;
	}

	for (int i = 0; i < K; i++) {
		cin >> T >> S >> P;
		queries[i] = { T, P, S };
	}
	sort(queries, queries + K, [](const Query& lv, const Query& rv) {
		return lv.t < rv.t;
	});

	dfs(1);

	fill(answer, answer + N + 1, MAX_T);
	fill(hi, hi + N + 1, K - 1);
	bool flag = true;

	while (flag) {

		fill(score, score + MAX, 0);
		fill(seg, seg + MAX * 4, 0);
		fill(lazy, lazy + MAX * 4, 0);

		for (int artist = 1; artist <= N; artist++) {
			if (songs[artist].size() && lo[artist] <= hi[artist]) {
				pbs[(lo[artist] + hi[artist]) / 2].push_back(artist);
			}
		}
		flag = false;
		for (int i = 0; i < K; i++) {
			auto [t, p, s] = queries[i];
			int root = order[s];
			int length = tree[s].descendants;
			update(root, root + length, p / (length + 1), 1, 1, N);

			while (!pbs[i].empty()) {
				int artist = pbs[i].back(); pbs[i].pop_back();

				for (auto song : songs[artist]) {
					int index = tree[song].index;
					score[artist] += sum(index, index, 1, 1, N);
					//if (score[artist] / songs[artist].size() > J) break;
				}

				ll target = J * songs[artist].size();
				if (target < score[artist]) {
					answer[artist] = min(answer[artist], queries[i].t);
					hi[artist] = i - 1;
				}
				else {
					lo[artist] = i + 1;
				}

				flag = true;
			}

		}


	}
	for (int i = 1; i <= N; i++) {
		int flag = answer[tree[i].artist] != MAX_T;
		cout << (flag ? answer[tree[i].artist] : -1) << '\n';
	}

	return 0;


}