ford-fulkerson 정당성 증명
이 포스트는 FordFulkerson의 정당성 증명에 관한 포스트입니다.
proof of correctness
cut 이란.
Min-cut 문제를 이용하여 증명을 하기 때문에 먼저 cut에 대해 알아보자
그래프 이론에서 cut이란 그래프의 정점을 두 개의 서로소 부분집합으로 분할 하는 것을 말한다. 어떤 컷이든 하나의 끝점이 있는 간선의 집합 cut-set을 결정한다.
flow netwrok에서는 s-t cut이라하며, 소스와 싱크를 다른 부분집합에 속하게 한다. 이 때 cut-set은 반드시 소스에서 싱크로가는 간선만을 포함한다. The capacity of an s–t cut은 cut-set의 포함되는 간선의 용량의 총합이다.
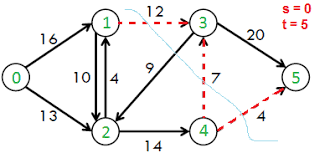
위 그림에서 s-t 컷의 용량은 \(12 + 7 + 4 = 33\)이다.
\(Thm\) of cut in flow network
- 컷의 유량은 소스에서 싱크로 가는 총 유량과 같다. 네트워크의 모든 유량은 \(s\)에 포함된 소스에서 흘러나와 \(t\)에 포함된 싱크로 흘러들어가기 때문이다.
- 컷의 유량은 용량과 같거나 더 작다. 이는 용량 제한 속성 때문이다.
- (용량 제한 속성) \(f(u, v) \leq c(u, v)\):
Min-cut Max-flow Theorem
네트워크에서 용량이 가장 작은 컷을 찾아내는 문제를 최소 컷(min cut) 문제라고 한다.
최소 컷 문제는 최대 유량 문제와 밀접하게 연관되어 있다.
만약 용량과 유량이 같은 컷 \(S, T\)가 존재한다 하자
\(Claim\): 컷 \(s, t\)는 항상 최소 컷이며, 소스에서 싱크로 가는 유량은 최대 유량이다.
\(Proof\)
\(s, t\)보다 용량이 작은 컷이 존재한다면 해당 컷에 대해 유량이 용량보다 크므로 모순이다. 이보다 많은 유량을 보내는 방법이 있을 경우에도 \(s, t\)에 대해 유량이 용량보다 크므로 모순이다. 따라서 컷 \(s, t\)는 항상 최소 컷이며, 소스에서 싱크로 가는 유량은 최대 유량이다.(최소 컷 최대 유량 정리)
정당성 증명
최소 용량 최대 유량 정리는 증가 경로가 존재하지 않는 유량 네트워크에서 용량과 유량이 같은 컷을 찾아내는 방법을 보여준다.
방법은 소스에서 잔여 용량이 있는 간선을 통해 갈 수 있는 정점들의 집합 \(S\)와 그럴 수 없는 정점 \(T\)로 정접의 집합을 나누는 것이다. 이와 같은 분류에서 소스는 항상 \(S\)에 속할 것이고 증가 경로가 존재하지 않기 때문에 싱크는 항상 \(T\)에 속할 것이다. 따라서, \(S,T\)는 유량 네트워크의 컷이 된다.
알고리즘이 시행된 후 \(S\)에 속한 정점에서 \(T\)에 속한 정점으로 가는 모든 간선의 잔여 용량은 0이다. 잔여 용량이 0이 아니라면 \(S\)에 포함되어야 하기 때문이다.
즉, 모든 간선에 대해 용량과 유량이 같다는 뜻이고 이 컷은 우리가 원하는 용량과 유량이 같은 컷이 된다. 네트워크의 최대 유량이다.
Refernce
- 구종만 지음, 알고리즘 문제 해결 전략, 인사이트, 32장
- https://en.wikipedia.org/wiki/Cut_(graph_theory)
- http://www.cs.toronto.edu/~lalla/373s16/notes/MFMC.pdf