조원빈

조원빈

Was mich nicht umbringt, macht mich stärker.

B-tree, index(작성중)

5 분 소요

데이터베이스 사용 중 자료구조에 대한 생각은 자연스레 떠오를 주제다. 단순히 어떤 구조가 효율적이라는 말은 수업에서 닳도록 들었다. 이번 포스트에서는 그것에 대한 직접적인 응용을 살펴보려 한다.

인덱스란?

인덱스란 단순히 생각하면 사전 순 정렬이다. 사전 같은 경우 미리 순서대로 정렬되어 있어 쉽게 찾을 수 있도록(데이터를 읽을 수 있도록) 도와준다. 마찬가지로 DBMS의 인덱스도 컬럼의 값을 주어진 순서로 미리 정렬해 보관한다.

자료구조를 어느정도 이해하고 있다면, 알 수 있듯이 위와 같이 미리 정렬된 저장구조는 읽기 성능을 끌어올리는 방법으로써 수정, 삭제, 삽입의 시간이 매우 크게 희생될 수 있다.

여기서도 알 수 있듯이 테이블의 인덱스를 하나 더 추가할지 말지는 데이터의 저장 속도를 어디까지 희생할 수 있는지, 읽기 속도를 얼마나 더 빠르게 만들어야 하는지의 여부에 따라 결정돼야 합니다. SELECT 쿼리 문장의 WHERE 조건절에 사용되는 컬럼이라고 전부 인덱스로 생성하면 데이터 저장 성능이 떨어지고 인덱스의 크기가 비대해져서 오히려 역효과만 불러올 수 있습니다.

B-tree

가장 일반적으로, 가장 먼저 사용된 인덱스 알고리즘으로써, 칼럼의 값을 변형하지 않고 원래의 값을 이용해 인덱싱하는 알고리즘이다. B+-Tree 혹은 B*-Tree가 자주 사용되며, 약자 B는 balanced를 의미한다.

구조 및 특성

B-Tree는 컬럼의 값을 변형시키지 않고 인덱스 구조체 내에서 항상 정렬된 상태로 유지하고 있다.

기본적으로 루트노드, 브랜치노드, 리프노드로 형성된 계층구조로 나뉘어져 있다. 또한, 자식 노드들은 구분자seperator를 가지는데 이는 부모노드가 가진 원소로서 BST에서 왼쪽과 오른쪽 범위를 결정해주는 노드의 value와 역할이 같다. 데이터베이스 내에서는 인덱스와 실제 데이터가 저장된 데이터는 따로 관리하는데, 인덱스의 리프 노드는 실제 데이터 레코드를 찾아가기 위한 주소 값을 가지고 있다.

대부분 RDBMS의 데이터 파일에서 레코드는 특정 기준으로 정렬되지 않고 임의의 순서대로 저장된다. 하지만 InnoDB에서는 클러스터링돼 디스크에 저장하는 것을 기본으로 하기에 프라이머리 키 순서대로 정렬한 후 저장된다. 다른 DBMS에서는 선택 사항이지만 별도의 옵션이 없다면 기본적으로 클러스터링 테이블이 생성된다.

InnoDB 테이블에서는 프라이머리 키에 의해 클러스터링되기 때문에 프라이머리 키값 자체가 주소 역할을 한다. 실제 MySQL 테이블의 인덱스는 항상 인덱스 컬럼 값과 주소 값(MyISAM의 레코드 아이디 값 또는 InnoDB의 프라이머리 키값)의 조합이 인덱스 레코드로 구성됩니다.

이미지

Advantages of B-tree usage for databases

  • 정렬된 키값 저장을 통해 쉽게 엑세스 가능
  • hierarchical index(계층적 인덱스?)를 사용한 디스크 엑세스 최소화
  • 삽입 삭제 속도 향상을 위한 partially full blocks 사용
  • 재귀적 알고리즘 사용을 통한 균형 트리 유지.

B-tree Properties

  1. 모든 리프 노드들은 같은 높이에 있다.
  2. order가 m인 경우 m-1개의 키와 m개의 자식 노드를 가질 수 있다.
  3. 모든 노드는 최대 m개의 노드를 자식으로 가질 수 있다.
  4. 루트 노드는 반드시 두 개 이상의 노드를 가지고 있어야 한다.
  5. 루트 노드와 리프 노드를 제외한 노드는 최소 두 개의(m/2) 자식 노드를 가진다.
  6. ROOT 노드를 제외한 모든 노드는 적어도 ⌊ M/2 ⌋ 개의 키를 가지고 있어야 한다.

탐색

이미지2

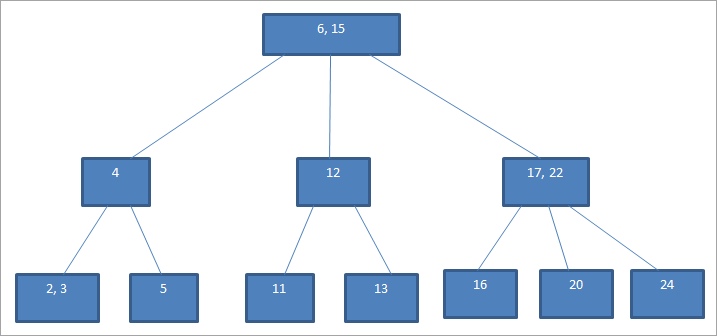
탐색과정은 이진 탐색 트리와 매우 흡사하다. 위 트리를 예시로 들어 \(3\)을 찾는다고 하자.

  1. \(3<\), \(3<15\) 이므로 왼쪽 서브 트리를 탐색한다.
  2. \(3<4\) 이므로 다시 왼쪽 서브 트리를 탐색한다.
  3. \(3>2\), \(3=3\)이므로 탐색을 종료한다.

위 탐색과정에서 알 수 있듯이 탐색은 트리의 높이에 의존한다. 보통 탐색 시간은 \(O(log N)\) 정도.

삽입

  1. 삽입할 위치를 탐색한다.
  2. 리프 노드가 \(m-1\)개 이하의 키를 가지고 있다면 오름차순으로 값을 삽입한다.
  3. 키가 \(m-1\)일 경우
    • 새로운 값을 오름차순으로 삽입한다.
    • 중간 값을 기준으로 두개의 노드로 나눈다.
    • 중간 값을 부모 노드로 보낸다.
    • 부모 노드의 키가 \(m-1\)개라면 적절한 리프 노드를 찾을 때까지 위 과정을 반복한다.
  4. 삽입이 완료된다.

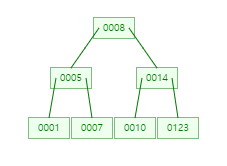
1 -> 10 -> 5 -> 14 -> 123 -> 7 -> 8 아래 이미지는 위 순서대로 삽입할 경우 생성되는 트리 구조이다.

이미지3

삭제

삭제 방식에는 두 가지가 존재.

  1. 삭제 후 invariants를 유지하도록 트리를 재구성
  2. Do a single pass down the tree, but before entering (visiting) a node, restructure the tree so that once the key to be deleted is encountered, it can be deleted without triggering the need for any further restructuring.

삭제할 경우 특이케이스는 아래와 같다.

  1. 브랜치 노드의 삭제할 원소가 자식 노드들의 구분자일 경우
  2. 원소를 삭제할 경우 해당 노드가 원소 최소개수와 자식 수를 만족하지 못할 경우

리프 노드 삭제

  1. 삭제할 값을 찾는다.
  2. 만약 값이 리프 노드에 있다면 그 노드를 삭제한다.
  3. b-tree 구조를 만족시키지 못할 경우 Rebalancing after deletion 항목에 따라 재구성한다.

브랜치 노드 삭제

브랜치 노드의 값은 항상 서브트리의 구분자로서 역할을 하기 때문에, 구분자의 역할을 대체할 필요가 있다. 여기서 알아야 할 점은 왼쪽 서브트리의 가장 큰 값은 항상 구분자보다 작고 오른쪽 서브트리의 가장 작은 값은 항상 구분자보다 크다는 점이다.

  1. 새로운 구분자를 찾는다. (왼쪽 서브트리 최대값 혹은 오른쪽 서브트리 최소값) 리프 노드에서 값을 제거 후 새로운 구분자를 추가한다.
  2. 리프 노드에서 삭제된 경우로 인해 트리의 균형이 깨졌다면 그 리프 노드부터 Rebalancing after deletion에 따라 재구성한다.

Rebalancing after deletion

재구성은 트리의 리프노드부터 시작하며 트리가 balanced 할 때까지 반복한다. 삭제로 인해 최소 원소를 가지지 못하게 노드는 모든 노드를 재분배하여 최소 원소를 맞추어야 한다. 보통 재분배는 최소 개수를 초과하는 형제로부터 가져오는 과정을 포함한다. 이러한 재분배를 회전rotation이라 하자. 만약 초과하는 형제 노드가 없을 경우에는 노드를 합친다.

  • deficient node의 오른쪽에 최소 개수를 초과하는 형제 노드를 가질 경우 왼쪽으로 회전한다.
    1. 부모 노드에서 구분자를 deficient node의 끝으로 복사한다(구분자가 하위 노드에 복사되어 최소 원소 개수를 만족하게 된다.)
    2. 형제 노드에서 첫번째 원소를 가져와 구분자 자리에 놓는다.
    3. 트리가 balanced 해진다.

오른쪽으로 회전 같은 경우에도 위와 같은 과정을 거친다.

  • 양쪽 형제 노드가 모두 최소 원소개수만을 만족한다면 부모 노드에 존재하는 구분자를 통해 합친다.
    1. 구분자를 왼쪽 노드 끝에 복사한다(이 때 왼쪽 노드는 deficient node거나 최소원소만을 만족하는 형제 노드일 수 있다)
    2. 오른쪽 노드의 모든 원소를 왼쪽으로 옮긴다(왼쪽 노드는 최대 원소개수를 만족하며 동시에 오른쪽 노드는 비어있다)
    3. 구분자와 오른쪽 노드를 삭제한다.
      • 부모노드가 루트이며 원소가 사라지면 기존 루트를 없애고 합쳐진 노드를 새로운 루트로 지정한다.
      • 위의 경우가 아니고, 부모 노드의 개수가 부족할 경우 부모 노드를 재배열한다.

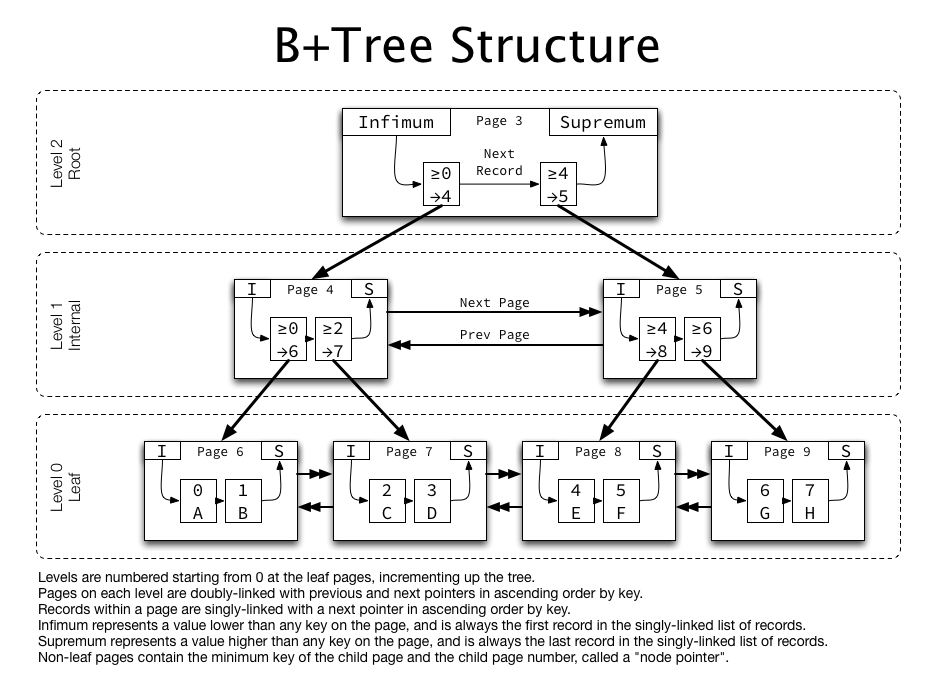
B+ Tree

B-트리는 특성상 순회 작업이 상당히 난감하다. B+ 트리는 색인구조에서 순차접근에 대한 문제의 해결책으로 제시되었다. (Wedekind, 1974) B-트리에서는 특정 key 값이 하나의 노드에서만 존재할 수 있지만 B+ 트리에서는 leaf 노드와 leaf의 부모 노드에서 공존할 수 있다. B+ 트리의 비단말 노드(not leaf)들은 데이터의 빠른 접근을 위한 인덱스 역할만 하기 때문이다. (index set 이라 불린다) 그리고 leaf 노드들은 연결 리스트 형태로 서로 연결되어 있고 이를 순차집합(sequence set)이라고 하며 오름차순으로 정렬이 되어 있다. 고로 B+ 트리는 (기존의 B-트리 + 데이터의 연결 리스트)로 구현된 색인구조라고 할 수 있다.

Theorem

B-트리의 변형 구조로 index 부분과 leaf 노드로 구성된 순차 data 부분으로 이루어진다. Index 부분의 key 값은 leaf에 있는 key 값을 직접 찾아 가는데 사용하고 모든 key 값은 leaf 노드에 나열된다. 즉, index 부분의 key 값도 leaf 노드에 다시 한 번 나열된다. Leaf 노드는 순차적으로 linked list를 구성하고 있어서 순차적 처리가 가능하다.

삽입

  1. B-tree와 거의 동일하게 이루어진다.
  2. 노드의 분열이 일어나면 중간 key 값이 부모 노드로 올라갈 뿐 아니라 새로 분열된 노드에도 포함되어야 한다.
  3. 새 노드는 leaf 노드끼리의 linked list에도 삽입되어야 한다.

삭제

  1. 재배치와 합병이 필요하지 않을 때는 leaf 노드에서만 삭제된다.
  2. Index 부분은 다른 key 값을 찾는데 사용될 수 있기 때문에 leaf node의 값이 삭제되어도 삭제하지 않는다.
  3. 재배치할 경우 index 부분의 node의 key 값은 변하지만 tree 구조는 변하지 않는다.
  4. 합병을 할 경우 index 부분에서도 key 값을 삭제한다.
Refernce
  • https://12bme.tistory.com/138
  • SQLD 개발자 가이드, http://www.dbguide.net/index.db
  • https://www.softwaretestinghelp.com/b-tree-data-structure-cpp/
  • https://www.cs.usfca.edu/~galles/visualization/BTree.html
  • https://matice.tistory.com/8
  • https://en.wikipedia.org/wiki/B-tree
  • https://arisu1000.tistory.com/27715
  • https://wangin9.tistory.com/entry/B-tree-B-tree

참고

오브젝트

2 분 소요

개요 해당 개시글은 책 오브젝트를 읽고 객체지향 설계에서 알아두면 좋을 것들을 정리한 게시글이다. 평소에 감으로 알고 있던 것들을 정리해두는 느낌이고, 독서 감상문 보다는 기억해둬야 할 것들을 작성자의 언어로 풀어쓴 글이라 생각하면 편할 것 같다.