dynamic programming
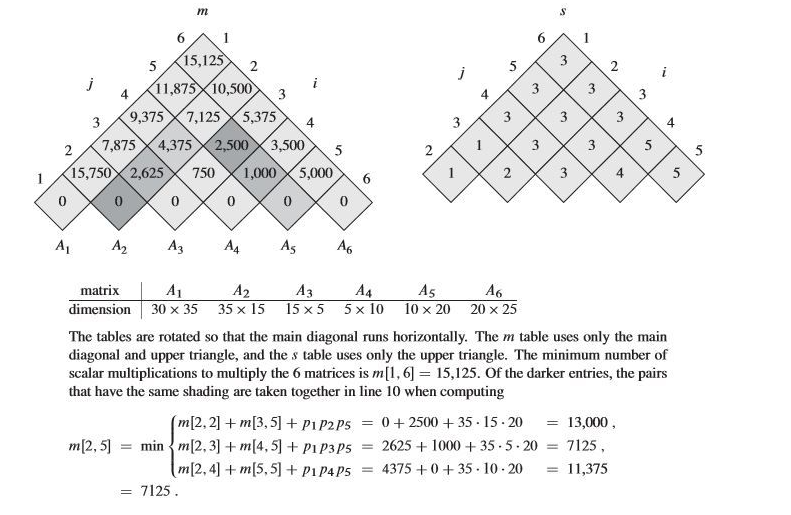
chained matrix multiplication
$input$: $d_0, d_1 … d_n$ $(\text{size of }M_i = d_{i-1} \times d_i)$
$output$: $D(i, j) = M_i \times M_{i+1} \times … \times M_j$ 의 최소비용
점화식
$\text{for all i}\in S, D(i,i) = 0$ $D(i, j) = min_{i \le k \le j}(D(i, k) + D(k + 1,j) + d_{i-1} \times d_k \times d_j$
알고리즘
edit distance
편집거리 알고리즘은 두 문자열의 유사도를 판단하는 알고리즘이다.
유사도를 판단하는 기준은 삽입, 삭제, 변경을 몇 번 진행해야 바꿀 수 있는지 최소값을 구하여 판단한다.
점화식
$ DP[m][n] = \begin{cases} DP[m - 1][n - 1] & \text{if }A[m] == B[n] \ min(DP[m - 1][n], DP[m][n - 1], DP[m - 1][n - 1]) + 1 & else \end{cases} $
$A$ 문자열의 $m$번째와 $B$ 문자열의 $n$번째 까지 문자열의 유사도를 나타내며 $A[m] == B[n]$일 경 $DP[m - 1][n - 1]$를 그대로 이어 받는다.
floyd warshall
변의 가중치가 음이거나 양인 가중그래프에서(음수 사이클이 없어야 한다.) 최단경로를 찾는 알고리즘이다.
점화식
알고리즘은 아래 점화식에 기반하여 동작한다. $D(k, i, j) = min(D(k - 1, i, k) + D(k - 1, k, j), D(k - 1, i, j))$
$D(k, i, j)$는 $1 .. k$ 까지의 정점을 사용하여 $i$에서 $j$로 갈 수 있는 최단거리를 뜻한다. 점화식에서는 $k - 1$까지의 정점을 사용한 후 중간에 $k$를 거쳐 최단거리를 구하는 방법과 기존 방법 중 더 최단경로를 선택한다.
알고리즘
for(int k = 1; k <= N; k++){
for(int i = 1; 1 <= N; i++){
for(int j = 1; j <= N; j++){
DP[i][j] = min(DP[i][k] + DP[k][j], DP[i][j]);
}
}
}
공간 복잡도를 $O(N^2)$으로 줄일 수 있는 이유는 $1 .. k - 1$의 정점을 사용하여 $k$로 가거나 도착하는 방법은 $1 .. k$일때도 같기 때문이다.
knapsack problem
문제 정의
도둑이 보석가게에 배낭을 메고 침입했다. 배낭의 최대 용량은 W이며, 이를 초과해서 보석을 담으면 배낭이 찢어질 것이다. 각 보석들의 무게와 가격은 알고 있다. 배낭이 찢어지지 않는 선에서 가격 합이 최대가 되도록 보석을 담는 방법은?
$input$: $W$, $(w_1,v_1), (w_2,v_2) … ,(w_n,v_n)$
$output$: the maximum value V less than or equal to W
점화식
$ DP[i][w] = \begin{cases} DP[i - 1][w] & \text{if }w_i > w \ max(v_i + DP[i-1][w-w_i], DP[i-1][w]) & else \end{cases} $
Fibonacci
점화식
$F_n = \begin{cases} 0 & \text{if }n = 0 \ 1 & \text{if }n = 1 \ F_{n-1} + F_{n-2} & \text{if }n > 1 \end{cases}$
알약
문제 정의
70세 박종수 할아버지는 매일 매일 약 반알을 먹는다. 손녀 선영이는 종수 할아버지에게 약이 N개 담긴 병을 선물로 주었다.
첫째 날에 종수는 병에서 약 하나를 꺼낸다. 그 다음, 그 약을 반으로 쪼개서 한 조각은 먹고, 다른 조각은 다시 병에 넣는다.
다음 날부터 종수는 병에서 약을 하나 꺼낸다. (약은 한 조각 전체 일 수도 있고, 쪼갠 반 조각 일 수도 있다) 반 조각이라면 그 약을 먹고, 아니라면 반을 쪼개서 한 조각을 먹고, 다른 조각은 다시 병에 넣는다.
종수는 손녀에게 한 조각을 꺼낸 날에는 W를, 반 조각을 꺼낸 날에는 H 보낸다. 손녀는 할아버지에게 받은 문자를 종이에 기록해 놓는다. 총 2N일이 지나면 길이가 2N인 문자열이 만들어지게 된다. 이때, 가능한 서로 다른 문자열의 개수는 총 몇 개일까?
점화식
$ DP[h][w] = \begin{cases} 1 & \text{if }h = 0 \ dp[h - 1][w + 1] & \text{else if }w = 0 \ dp[h - 1][w + 1] + dp[h][w - 1] & \text{else } \end{cases} $
코드
#include<iostream>
using namespace std;
const int MAX = 30 + 1;
int N, input;
long long dp[MAX][MAX];
int main() {
//FAST IO
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
//DP
for (int h = 0; h <= 30; h++) {
for (int w = 0; w <= 30; w++) {
if (h == 0) {
dp[h][w] = 1;
}
else if (w == 0) {
dp[h][w] = dp[h - 1][w + 1];
}
else {
dp[h][w] = dp[h - 1][w + 1] + dp[h][w - 1];
}
}
}
while (true) {
cin >> N;
if (N == 0) break;
cout << dp[N][0] << '\n';
}
}
팰린드롬?
문제 정의
명우는 홍준이와 함께 팰린드롬 놀이를 해보려고 한다.
먼저, 홍준이는 자연수 N개를 칠판에 적는다. 그 다음, 명우에게 질문을 총 M번 한다.
각 질문은 두 정수 S와 E(1 ≤ S ≤ E ≤ N)로 나타낼 수 있으며, S번째 수부터 E번째 까지 수가 팰린드롬을 이루는지를 물어보며, 명우는 각 질문에 대해 팰린드롬이다 또는 아니다를 말해야 한다.
https://www.acmicpc.net/problem/10942
점화식

코드
#include<iostream>
using namespace std;
int dp[2001][2001], N, S, E, M, n[2001];
int main() {
//FAST IO
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> N;
for (int i = 0; i < N; i++) {
cin >> n[i];
}
//dp
//It should be noted here that the order in which DP matrices are filled is diagonal,
//which creates a lower triangulation matrix.
for (int diff = 0; diff < N; diff++) {
for (int s = 0, e = s + diff; s < N; s++, e++) {
if (s == e) {
dp[s][e] = true;
}
else if (e - s == 1) {
dp[s][e] = (n[e] == n[s]);
}
else {
dp[s][e] = (n[e] == n[s] && dp[s + 1][e - 1]);
}
}
}
cin >> M;
for (int i = 0; i < M; i++) {
cin >> S >> E;
cout << dp[S - 1][E - 1] << '\n';
}
}
고층 빌딩
문제 정의
상근이가 살고있는 동네에는 빌딩 N개가 한 줄로 세워져 있다. 모든 빌딩의 높이는 1보다 크거나 같고, N보다 작거나 같으며, 같은 높이를 가지는 빌딩은 없다. 상근이는 학교 가는 길에 가장 왼쪽에 서서 빌딩을 몇 개 볼 수 있는지 보았고, 집에 돌아오는 길에는 가장 오른쪽에 서서 빌딩을 몇 개 볼 수 있는지 보았다.
상근이는 가장 왼쪽과 오른쪽에서만 빌딩을 봤기 때문에, 빌딩이 어떤 순서로 위치해있는지는 알 수가 없다.
빌딩의 개수 N과 가장 왼쪽에서 봤을 때 보이는 빌딩의 수 L, 가장 오른쪽에서 봤을 때 보이는 빌딩의 수 R이 주어졌을 때, 가능한 빌딩 순서의 경우의 수를 구하는 프로그램을 작성하시오.
예를 들어, N = 5, L = 3, R = 2인 경우에 가능한 빌딩의 배치 중 하나는 1 3 5 2 4이다
점화식
$ dp[N][L][R] = ( dp[N - 1][L - 1][R] + dp[N - 1][L][R - 1] + dp[N - 1][L][R] * (N - 2) ) \pmod p; $
코드
#include<iostream>
#define MOD %
using namespace std;
const int PRIME = 1000000007, MAX = 100 + 5;
long long dp[MAX][MAX][MAX];
int N, R, L;
int memo(int n, int l, int r) {
if (l == 0 || r == 0) return 0;
long long& ret = dp[n][l][r];
if (ret != -1) return ret;
return ret = (memo(n - 1, l - 1, r) + memo(n - 1, l, r - 1) + memo(n - 1, l, r) * (n - 2)) MOD PRIME;
}
int main() {
cin >> N >> R >> L;
//Recurrence relation
//dp[N][L][R] = dp[N - 1][L - 1][R] + dp[N - 1][L][R - 1] + dp[N - 1][L][R] * (N - 2);
dp[1][1][1] = 1;
for (int n = 2; n <= N; n++) {
for (int l = n; l > 0; l--) {
for (int r = 1; l + r <= n + 1; r++) {
dp[n][l][r] = dp[n - 1][l - 1][r] + dp[n - 1][l][r - 1] + dp[n - 1][l][r] * (n - 2);
dp[n][l][r] = dp[n][l][r] MOD PRIME;
}
}
}
cout << dp[N][L][R];
}