Pollard's rho algorithm
Introduction
이번 포스트에서 다룰 알고리즘은 폴라드 $\rho$ 알고리즘이다. 폴라드 $\rho$ 알고리즘은 빠른 소인수 분해를 위한 알고리즘이다.
백준에 큰 수 소인수분해 4149 문제 풀이와 함께 진행하겠다.
Core ideas
소인수 분해하려는 숫자 $n = pq$에서 $p$는 자명하지 않은 인수라고 가정하자. 다항식을 $n$으로 나누는 연산 $g(x) = (x^2 + 1)\text{ mod n}$은 암호학에 유사난수 수열을 생성(PRG)할 때 사용된다.
이때 시작값을 적당히 2로 설정하면
$x_1 = g(2),,x_2=g(g(2)),,x_3=g(g(g(2)))$
위와 같은 형태로 수열이 생성된다. 이를 ${x_k}$라 하자. 그러면 이 수열은 다른 수열 ${x_k ,mod,p}$ 과 관련이 있다. 하지만 $p$가 사전에 주어지지 않았기 때문에, 두 번째 수열은 위 알고리즘으로 계산 불가능하다. 여기서 첫 번째 수열과 두 번째 수열의 관계가 폴라드 로 알고리즘의 핵심 아이디어다.
이 수열에 나오는 수의 개수는 유한하기 때문에, $n$의 나머지 수열 ${x_k}$와 ${x_k ,mod,p}$는 언젠가 반복된다. 이 수열을 완전한 난수라고 가정하면 birthday pardox에 의해 이 수열이 반복되기 전까지 나오는 서로 다른 $x_k$의 개수는 대략 $O(\sqrt{n})$이다. (여기서 $N$은 가능한 값의 개수이다.) 따라서, 수열 ${x_k ,mod,p}$은 수열 ${x_k}$보다 먼저 반복된다.
각각의 수열을 유향 그래프로 표현한다면 그리스 문자 $\rho$와 같이 생겨서 폴라드 로 알고리즘이라 붙인 것이다.
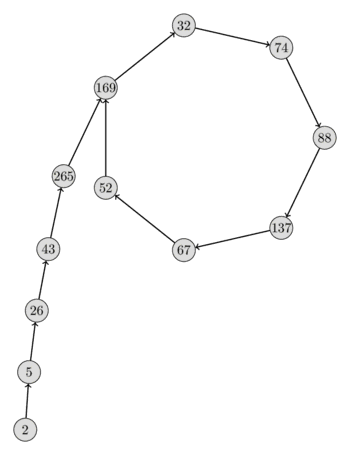
그렇다면, 두 수열의 관계를 어떻게 이용하여 우리는 인수 p를 찾아내는 것일까? 알고리즘은 아래와 같이 동작한다.
- 위 수열에서 나오는 반복을 순환 찾기 알고리즘으로 찾는다.
- 먼저 두 수 $x_i$와 $x_j$를 정한다. $x_i \equiv x_j \pmod p$를 만족 시 $p = k(x_i - x_j) ,, k \in \mathbb{N}$가 성립한다.
- $gcd(x_i - x_j, n)$이 1이 아니라면 수열 ${x_k ,mod,p}$는 사이클이 있다는 것을 의미하고, $x_i - x_j$이 p의 배수 혹은 0이 되어야한다.
- $gcd(x_i - x_j, n)$는 결국 $n$ 혹은 $p$를 값으로 가지게되고, $p$를 구할 수 있다.
Algorithm
Floyd’s Cycle Detection Algorithm
우선 수열 ${x_k ,mod,p}$의 사이클을 찾는 알고리즘은, 플로이드 알고리즘을 통해 구현한다.
이는 Two Pointer를 이용하며, 이 포인터는 서로 다른 속도로 시퀀스를 탐색한다. 매 반복마다, 첫 포인터는 한 칸을 움직이고 두번째 포인터는 두 칸을 움직인다. 만약 사이클 길이가 $\lambda$이고 사이클이 시작하는 곳의 첫 인덱스가 $\mu$일 경우 시간복잡도는 $O(\mu + \lambda)$다.
This algorithm is also known as tortoise and the hare algorithm, based on the tale in which a tortoise (here a slow pointer) and a hare (here a faster pointer) make a race.
플로이드 알고리즘은 재귀적으로 비교하는 두 인자에 진행속도에 차이를 두어 만약 사이클이 존재할 경우 둘이 만날 수 밖에 없도록 하는 것이다.
pseudo code
function floyd(f, x0):
tortoise = x0
hare = f(x0)
while tortoise != hare:
tortoise = f(tortoise)
hare = f(f(hare))
return true
implementation
...
do {
if (g == n) {
x = y = rand() % n + 1;
c = rand() % n + 1;
g = 1;
}
x = f(x);
y = f(f(y));
ull sub = x > y ? x - y : y - x;
g = gcd(n, sub);
} while (g == 1);
...
Brent’s algorithm
__int128_t 타입을 사용하지 않을 경우 곱셈 연산을 매우 느리게 진행해야하는데, 이에 따라 플로이드 알고리즘 만으로는 제한시간 내에 풀기 어려울 수 있어 새로운 알고리즘 도입이 필요했다.
위 알고리즘은 플로이드 알고리즘과 비슷하다. 투 포인터를 사용하지만 $2^i$만큼 전진시킨다. $2^i$가 $\mu, \lambda$보다 크면, 사이클을 찾을 수 있다. 자세한 코드는 최종 코드에서 확인하길 바란다.
pseudo code
function floyd(f, x0):
tortoise = x0
hare = f(x0)
l = 1
while tortoise != hare:
tortoise = hare
repeat l times:
hare = f(hare)
if tortoise == hare:
return true
l *= 2
return true
Miller-Rabin primality test
여기서 주의해야할 점은 폴라드 로 알고리즘이 소인수가 아닌 인수분해 알고리즘이란 점이다. 즉, 우리가 구한 $p$가 소수인지를 빠르게 판단해야 한다. 이는 밀러라빈 소수 판정법을 통해 구현해야 한다.
밀러-라빈 소수 판정법은 확률적 판별 알고리즘이다. 페르마 테스트와 더불어 몇 개의 인자를 넣어 확률적으로 아닌지를 판단해야한다.
Lemma
알고리즘 설명 전에 우선 보조정리부터 소개하겠다.
소수 $p$에 대해 $x^2 \equiv \pmod p$이면 $x \equiv 1 \pmod p$ 거나 $x \equiv -1 \pmod p$이다.
$Proof$: 합동식 정의에서 $x^2-1 = (x+1)(x-1)$은 $p$의 배수이고, $x+1$과 $x-1$ 둘 중 하나는 $p$의 배수여야한다.
여기서 수학적 직관이 어느정도 있는 사람이라면, 과연 위 합동식이 해를 두 개만 가지는지에 대해 의문을 들 수 있다. 먼저 정답을 말하자면 그렇다. 우리는 좀 더 일반적인 상황에서 아래와 같은 증명도 가능하다!
$\mathbb{Z}_p$ 상에서 다항식 차수로 $n$을 가지는 $f(x)$는 최대 $n$개의 해를 가진다.
이 증명은 링크에서 확인 가능하다.
Mathematical concepts
$Claim$: $n$을 2보다 큰 소수라 하자. 그러면 아래 두 조건 중 하나를 반드시 만족한다.
$a^d \equiv 1 \pmod n$
$a^{2^rd} \equiv -1 \pmod n \text{, for some }0 \le r \le s-1$
$Proof$: 페르마 소정리에 따라 소수 $n$에 대해 $a$는 아래를 만족한다.
$a^{n-1} \equiv 1 \pmod n$
여기서 어떤 수 $n$가 홀수라면, $n-1$은 짝수다. 짝수는 2의 거듭제곱을 약수로 가지므로 다음과 같이 정의된다.
$n-1 = 2^sd, , \text{d is odd}$
따라서, $a^{n-1} \equiv 1 \pmod n$은 아래와 같이 변형할 수 있다.
$$\begin{align} a^{2^sd} & = (a^{2^{s-1}d}-1)(a^{2^{s-1}d} + 1) \ &= (a^{2^{s-2}d} - 1)(a^{2^{s-2}d} + 1)(a^{2^{s-1}d} + 1) \ … \ &= (a^d - 1)(a^{2d} + 1)…(a^{2^{s-3}d} + 1)(a^{2^{s-2}d} + 1)(a^{2^{s-1}d} + 1) \end{align}$$
따라서, 두 조건 중 하나를 만족할 경우 $n$은 확률적으로 소수임을 알 수 있다.
소수 판정 코드
...
ull pow_with_mod(ull a, ull b, ull mod) {
a = a % mod;
ull ret = 1;
while (b > 0) {
if (b % 2 == 1) {
ret = (__int128_t)ret * a % mod;
}
a = (__int128_t)a * a % mod;
b = b >> 1;
}
return ret;
}
bool miller_rabin_primality_test(ull n, ull a) {
ull d = n - 1;
while (d % 2 == 0) {
if (pow_with_mod(a, d, n) == n - 1) {
return true;
}
d = d >> 1;
}
ull pow_of_a_d = pow_with_mod(a, d, n);
return pow_of_a_d == n - 1 || pow_of_a_d == 1;
}
bool is_prime(ull n) {
if( n <= 1 ) return false;
if (n <= 1000000000ULL) {
for (ull i = 2; i * i <= n; i++) {
if (n % i == 0) {
return false;
}
}
return true;
}
for (ull a : {2, 325, 9375, 28178, 450775, 9780504, 1795265022}) {
if (!miller_rabin_primality_test(n, a)) {
return false;
}
}
return true;
}
...
최종 코드
#include<iostream>
#include<vector>
#include<algorithm>
using ull = unsigned long long;
using namespace std;
vector<ull> factors;
ull n;
//NOTICE: __int128_t type only use in gcc
//return a^b % mod with divide and conquer
ull pow_with_mod(ull a, ull b, ull mod) {
a = a % mod;
ull ret = 1;
while (b > 0) {
if (b % 2 == 1) {
ret = (__int128_t)ret * a % mod;
}
a = (__int128_t)a * a % mod;
b = b >> 1;
}
return ret;
}
bool miller_rabin_primality_test(ull n, ull a) {
ull d = n - 1;
while (d % 2 == 0) {
if (pow_with_mod(a, d, n) == n - 1) {
return true;
}
d = d >> 1;
}
ull pow_of_a_d = pow_with_mod(a, d, n);
return pow_of_a_d == n - 1 || pow_of_a_d == 1;
}
bool is_prime(ull n) {
if( n <= 1 ) return false;
if (n <= 1000000000ULL) {
for (ull i = 2; i * i <= n; i++) {
if (n % i == 0) {
return false;
}
}
return true;
}
for (ull a : {2, 325, 9375, 28178, 450775, 9780504, 1795265022}) {
if (!miller_rabin_primality_test(n, a)) {
return false;
}
}
return true;
}
ull abs(ull a) {
return a > 0 ? a : -1 * a;
}
//Euclidean algorithm
ull gcd(ull a, ull b) {
if (a < b) swap(a, b);
if (b == 0) return a;
return gcd(b, a % b);
}
void factorize(ull n) {
if (n <= 1) return;
if (is_prime(n)) {
factors.push_back(n);
return;
}
ull x = 2, q = 1, g = 1, xs, y, c = rand() % 10 + 1;
auto f = [=](ull x) {
return ((__int128_t)x * x + c) % n;
};
//Brent's Algorithm: Faster than Floyd's cycle-fiding algorithm
int m = 128;
int l = 1;
while (g == 1) {
y = x;
for (int i = 1; i < l; i++) {
x = f(x);
}
int k = 0;
while (k < l && g == 1) {
xs = x;
for (int i = 0; i < m && i < l - k; i++) {
x = f(x);
q = (__int128_t)q * abs(y - x) % n;
}
g = gcd(q, n);
k += m;
}
l *= 2;
}
if (g == n) {
do {
xs = f(xs);
g = gcd(abs(xs - y), n);
} while (g == 1);
}
factorize(g);
factorize(n / g);
}
int main() {
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
cin >> n;
factorize(n);
sort(factors.begin(), factors.end());
for (auto factor : factors) {
cout << factor << '\n';
}
}