Hammer's Blog

Prooving Ford Fulkerson correctenss

cut 이란.

Min-cut 문제를 이용하여 증명을 하기 때문에 먼저 cut에 대해 알아보자

그래프 이론에서 cut이란 그래프의 정점을 두 개의 서로소 부분집합으로 분할 하는 것을 말한다. 어떤 컷이든 하나의 끝점이 있는 간선의 집합 cut-set을 결정한다.

flow netwrok에서는 s-t cut이라하며, 소스와 싱크를 다른 부분집합에 속하게 한다. 이 때 cut-set은 반드시 소스에서 싱크로가는 간선만을 포함한다. The capacity of an s–t cut은 cut-set의 포함되는 간선의 용량의 총합이다.

이미지1

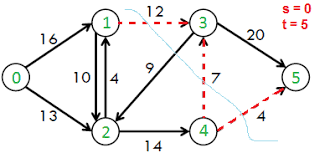
위 그림에서 s-t 컷의 용량은 $12 + 7 + 4 = 33$이다.

$Thm$ of cut in flow network

  1. 컷의 유량은 소스에서 싱크로 가는 총 유량과 같다. 네트워크의 모든 유량은 $s$에 포함된 소스에서 흘러나와 $t$에 포함된 싱크로 흘러들어가기 때문이다.
  2. 컷의 유량은 용량과 같거나 더 작다. 이는 용량 제한 속성 때문이다.

Min-cut Max-flow Theorem

네트워크에서 용량이 가장 작은 컷을 찾아내는 문제를 최소 컷(min cut) 문제라고 한다. 최소 컷 문제는 최대 유량 문제와 밀접하게 연관되어 있다.

만약 용량과 유량이 같은 컷 $S, T$가 존재한다 하자
$Claim$: 컷 $s, t$는 항상 최소 컷이며, 소스에서 싱크로 가는 유량은 최대 유량이다.

$Proof$
$s, t$보다 용량이 작은 컷이 존재한다면 해당 컷에 대해 유량이 용량보다 크므로 모순이다. 이보다 많은 유량을 보내는 방법이 있을 경우에도 $s, t$에 대해 유량이 용량보다 크므로 모순이다. 따라서 컷 $s, t$는 항상 최소 컷이며, 소스에서 싱크로 가는 유량은 최대 유량이다.(최소 컷 최대 유량 정리)

정당성 증명

최소 용량 최대 유량 정리는 증가 경로가 존재하지 않는 유량 네트워크에서 용량과 유량이 같은 컷을 찾아내는 방법을 보여준다.

방법은 소스에서 잔여 용량이 있는 간선을 통해 갈 수 있는 정점들의 집합 $S$와 그럴 수 없는 정점 $T$로 정접의 집합을 나누는 것이다. 이와 같은 분류에서 소스는 항상 $S$에 속할 것이고 증가 경로가 존재하지 않기 때문에 싱크는 항상 $T$에 속할 것이다. 따라서, $S,T$는 유량 네트워크의 컷이 된다.

알고리즘이 시행된 후 $S$에 속한 정점에서 $T$에 속한 정점으로 가는 모든 간선의 잔여 용량은 0이다. 잔여 용량이 0이 아니라면 $S$에 포함되어야 하기 때문이다.

즉, 모든 간선에 대해 용량과 유량이 같다는 뜻이고 이 컷은 우리가 원하는 용량과 유량이 같은 컷이 된다. 네트워크의 최대 유량이다.

Refernce

#Database